Principio de indeterminación de Heisenberg
El hecho de que cada partícula lleva asociada consigo una onda, impone restricciones en la capacidad para determinar al mismo tiempo su posición y su velocidad. Este principio fué enunciado por W. Heisenberg en 1927.
 |
| Imagen tomada de: http://www.nucleares.unam.mx/~vieyra/node20.html |
Es natural pensar que si una partícula esta localizada, debemos poder
asociar con ésta un paquete de ondas mas o menos bien localizado.
Un paquete de ondas se construye mediante la superposición de un número
infinito de ondas armónicas de diferentes frecuencias.
En un instante de tiempo dado, la función de onda asociada con un paquete
de ondas esta dado por
 |
| Imagen tomada de: http://www.nucleares.unam.mx/~vieyra/node20.html |
y donde la integral representa la suma de ondas con frecuencias (o número
de ondas) que varian desde cero a mas infinito ponderadas mediante el factor
g(k).
El momento de la partícula y el número de ondas estan relacionados
ya que
 |
| Imagen tomada de: http://www.nucleares.unam.mx/~vieyra/node20.html |
de lo cual se deduce que
 |
| Imagen tomada de: http://www.nucleares.unam.mx/~vieyra/node20.html |
Queda claro que para localizar una partícula es necesario sumar todas
las contribuciones de las ondas cuyo número de onda varia entre cero e
infinito y por lo tanto el momento
Para ilustrar lo anterior hemos indicado en la siguiente figura diferentes
tipos de paquetes de onda y su transformada de Fourier que nos dice
como estan distribuidas las contribuciones de las ondas con número de ondas
k dentro del paquete.
 |
| Imagen tomada de: http://www.nucleares.unam.mx/~vieyra/node20.html |
En el primer caso vemos que un paquete de ondas bien localizado en el
espacio x, tiene contribuciones practicamente iguales de todas las ondas
con número de ondas k.
En el segundo caso vemos que si relajamos un poco la posición del paquete de ondas, también es posible definir el número de ondas (o el momento) de la partícula.
En el último caso vemos que para definir bien el momento
Es posible determinar el ancho, o la incertidumbre, del paquete de ondas tanto en el espacio normal
 |
| Imagen tomada de: http://www.nucleares.unam.mx/~vieyra/node20.html |
El principio de incertidumbre nos dice que hay un límite en
la precisión con el cual podemos determinar al mismo tiempo la
posición y el momento de una partícula.
La expresión matemática que describe el principio de incertidumbre de Heisenberg es
 |
| Imagen tomada de: http://www.nucleares.unam.mx/~vieyra/node20.html |
Si queremos determinar con total precisión la posición:
 |
| Imagen tomada de: http://www.nucleares.unam.mx/~vieyra/node20.html |
De la desigualdad para el principio de incertidumbre verificamos
entonces que
 |
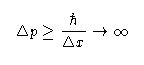| Imagen tomada de: http://www.nucleares.unam.mx/~vieyra/node20.html |
Es decir, que la incertidumbre en el momento es infinita.
Bibliografía;
La información fue tomada el día: 28/06/2017
De las páginas: http://www.nucleares.unam.mx/~vieyra/node20.html
Comentarios
Publicar un comentario